강의
확률
"표본집합"은 실험의 결과로 발생하는 모든 결과의 집합 입니다.
"확률"은 집합의 부분집합을 실수값에 대응시키는 함수 입니다.
확률변수
"확률변수"(Random Variable)은 표본집합의 원소를 실수갑에 대응시키는 함수 입니다.

"연속확률변수"(Continuous Random Variable)은 누적분포함수를 가진 확률변수에 대해 다음 식을 만족하는 확률밀도함수가 존재하는 확률변수 입니다.


확률변수 성질
- 덧셈법칙(Sum Rule)

- 곱셈법칙(Product Rule)

- 베이즈 확률(Bayes)
- 사후확률(Posterior)
- 사전확률(Prior)
- 가능도 혹은 우도(Likelihood)
- 경계확률(Nomalization)

기댓값과 분산
"기댓값"(Expectation)은 확률분포 하에서 함수의 평균값 입니다.
- 이산확률분포

- 연속확률분포

- 근사

- 다변수
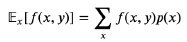
- 조건부 기댓값
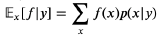
"분산"(Variance)는 밀도함수의 값들이 기댓값으로부터 흩어져 있는 정도 입니다.

"공분산"(Covariance)는 두 개의 확률변수에 대한 공통 분산 입니다.

확률 해석 관점
- 빈도주의(Frequentist) : 반복가능한 사건들의 빈도수에 기반
- 베이지안(Bayesian) : 불확실성을 정량적으로 표현
'데브코스 TIL > Machine Learning' 카테고리의 다른 글
| 기초 확률 분포 (0) | 2024.01.31 |
|---|---|
| 기초 선형대수 (0) | 2024.01.30 |
| 머신러닝 소개 (0) | 2024.01.29 |