강의
기본 표기법
- 벡터
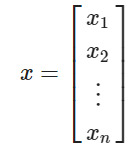
import numpy as np
x = np.array(list)- 행렬
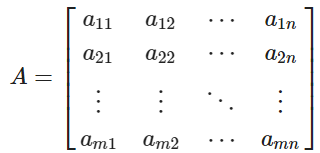
import numpy as np
A = np.array([
list1,
list2
...
])
행렬의 곱셈

- 벡터 X 벡터


import numpy as np
# 내적
x = np.array(list1)
y = np.array(list2)
x.dot(y)
# 외적
x = np.expand_dims(x, axis=1)
y = np.expand_dims(y, axis=0)
np.matmul(x,y)- 행렬 X 벡터

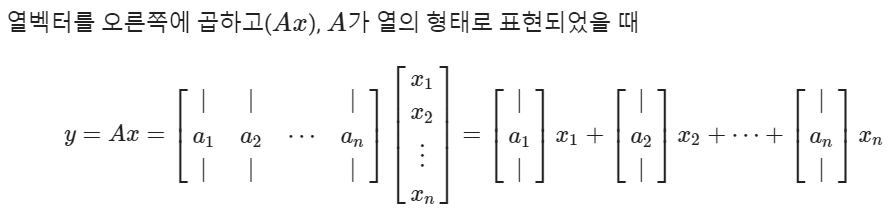

- 행렬 X 행렬
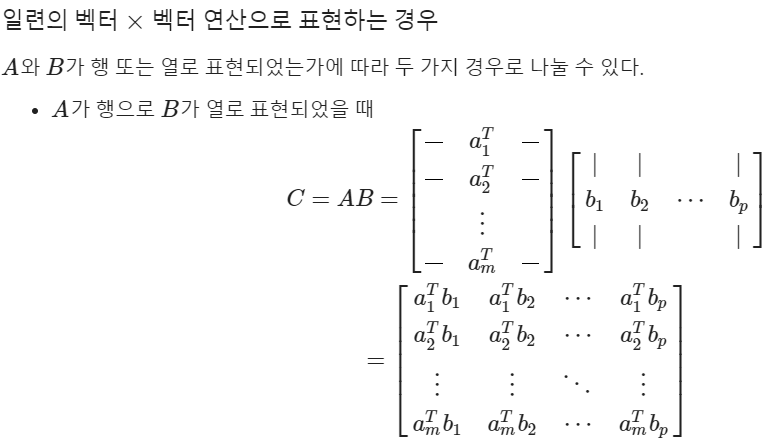

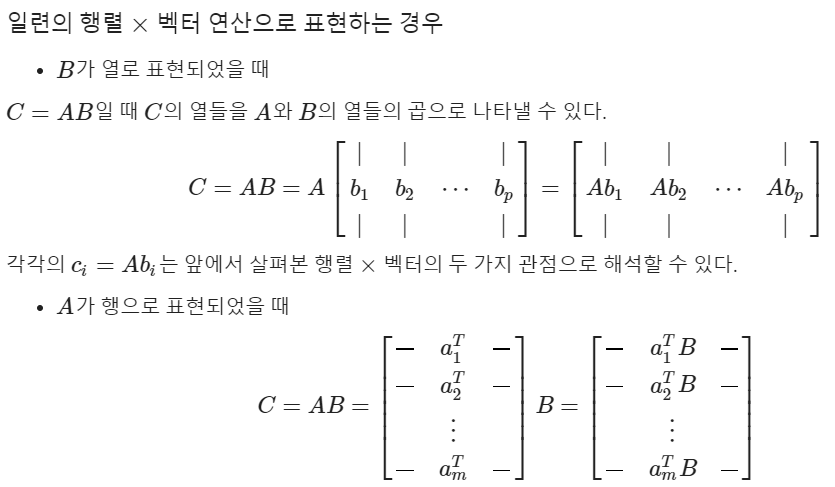
특수 행렬
- 정방행렬(Square Matrix) : 행과 열의 개수 동일
- 상삼각행렬(Upper Triangular Matrix) : 주대각선 아래 원소의 값이 모두 0인 정방행렬
- 하삼각행렬(Lower Triangular Matrix) : 주대각선 위 원소의 값이 모두 0인 정방행렬
- 대각행렬(Diagonal Matrix) : 주대각선 외의 모든 원소의 값이 0인 정방행렬
import numpy as np
np.diag(D) # 주대각선 값- 단위행렬(Identity Matrix) : 주대각선의 모든 원소의 값이 1인 대각행렬
import nupmy as np
I = np.eye(n)
연산
- 전치(Transpose)
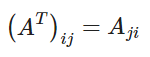
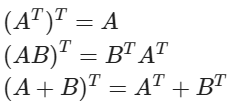
A.T- 대칭(Symmetic) : 행렬이 자신의 정방행렬과 동일
- 반대칭(Anti-Symmetric) : 행렬이 자신의 부호가 반대인 정방행렬과 동일
- 대각합(Trace) : 주대각선의 모든 원소들의 합
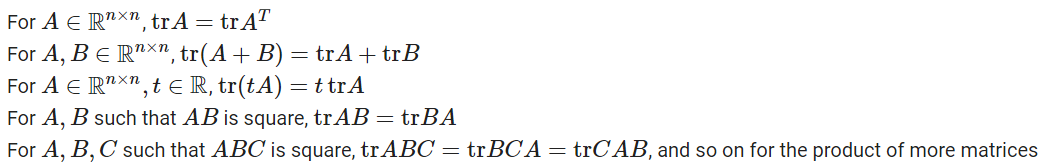
import numpy as np
np.trace(A)- 놈(Norms) : 벡터의 길이
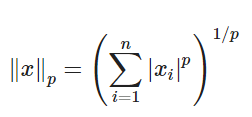
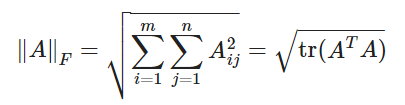

LA.norm(A)
선형독립
"선형독립"(Linear Independent)는 벡터들의 집합에 속해 있는 어떤 벡터도 나머지 벡터들의 선형조합으로 나타낼 수 없는 경우를 말합니다.
"종속"(Dependent)은 어떠한 벡터가 나머지 벡터들의 선형조합으로 나타낼 수 있는 경우를 말합니다.
- Column Rank : 행렬의 열의 부분집합 중 가장 큰 선형독립인 집합의 크기
- Row Rank : 행렬의 행의 부분집합 중 가장 큰 선형독립인 집합의 크기
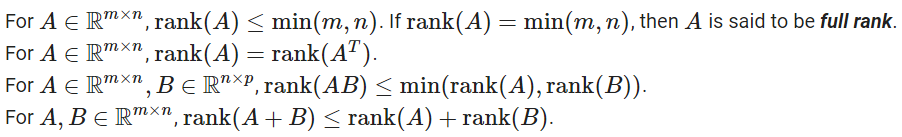
LA.matrix_rank(A)
역행렬
"역행렬"(The Inverse)는 다음을 식을 만족하는 정방행렬 입니다.
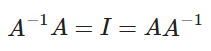

LA.inv(A)
직교 행렬
"직교"(Orthogonal)는 다음 식을 만족하는 경우를 말합니다.
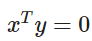
"직교행렬"은 모든 열이 서로 직교이고 정규화된 정방행렬 입니다.
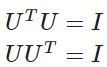
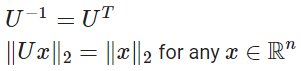
공간
"생성"(Span)은 벡터의 집합이 다음 식을 만족하는 경우를 말합니다.
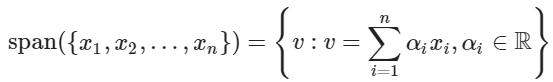
"치역"(Range)는 행렬의 모든 열들에 대한 생성 입니다.
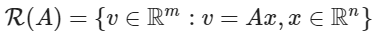
"영공간"(Nullspace)은 행렬과 곱해졌을 때 0이 되는 모든 벡터들의 집합 입니다.

"투영"(Projection)은 치역 위에서 벡터가 다음 식을 만족하는 것을 말합니다.
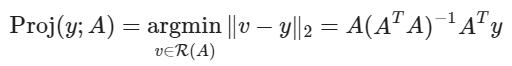
행렬식
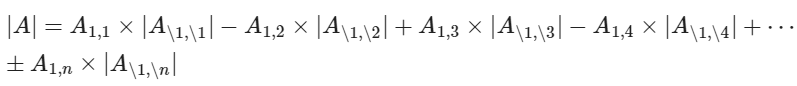
LA.det(A)
이차형식
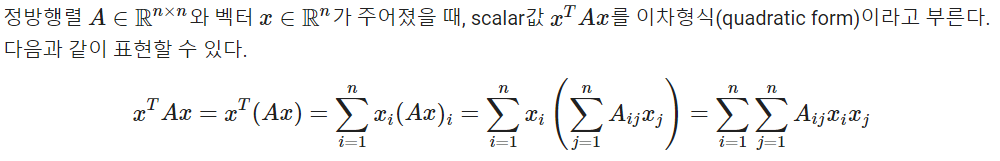
고유값과 고유벡터


eigenvalues, eigenvectors = LA.eig(A)
행렬미분(Matrix Calculus)
- The Gradient
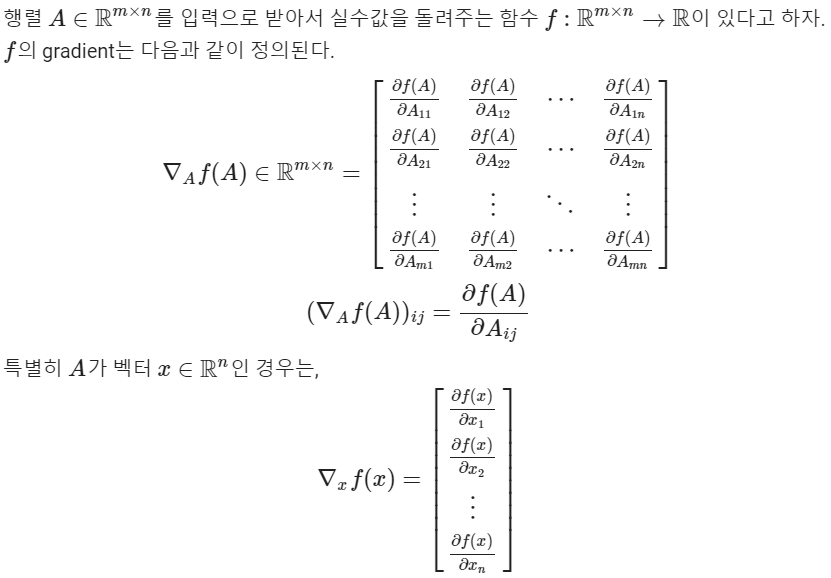
- The Hessian
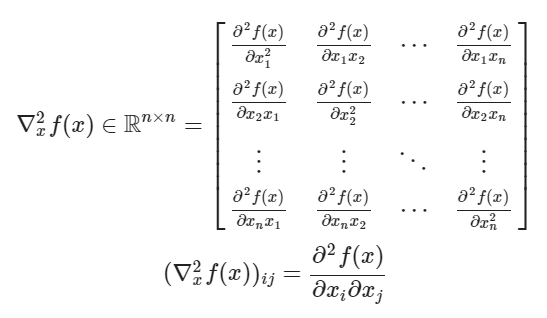
적용예시
- 최소제곱법(Laest Squares)
- 고유값과 최적화문제(Eigenvalues as Optimization)
- Autoencoder와 Principle Components Analysis(PCA)
- 최적의 D 찾기
'데브코스 TIL > Machine Learning' 카테고리의 다른 글
| 기초 확률 분포 (0) | 2024.01.31 |
|---|---|
| 기초 확률 (0) | 2024.01.31 |
| 머신러닝 소개 (0) | 2024.01.29 |